Time, Clocks, and the Ordering of Events in a Distributed System, Lamport, 1978

2020/10/06

本篇总结学习了1978年Leslie Lamport发表在 Communications of the ACM 上的论文 Time, Clocks, and the Ordering of Events in a Distributed System。论文对分布式系统中的时间，时钟等概念做了深入的讨论，提出了“Happened Before”，“逻辑时钟”，“物理时钟”，“State Machine”等重要概念与算法，是分布式领域不能不读的经典论文。

1. 问题

在进入正题之前，首先让我们考虑如下问题：

$A$，$B$ 两人各自带着手表，在咖啡厅中喝咖啡，

假定两人都是诚实的，我们能说 $A$ 在 $B$ 之前喝完咖啡吗？

结论是不一定。由于我们并不知道两人的手表时间是否“准确”，即便两人诚实地说出了自己喝完咖啡时手表的读数，也并不能由此推论出孰先孰后。那么如果情形变成如下这样，结论又是如何呢？

在这种情形下，我们可以得知 $A$ 在通话前喝完咖啡，$B$ 在通话后喝完咖啡，故而必然有 $A$ 在 $B$ 之前喝完咖啡。一通电话使得彼此独立的两个时间体系产生了确定性的先后关系。

由上面的例子可见，我们通常使用的时钟读数、时间戳等概念并不能准确地刻画出事件发生的先后顺序。而在分布式系统中，事件发生的先后常常扮演着各种算法的“关键角色”。那么我们如何准确地刻画这种顺序，或是设计我们的时钟，从而准确的刻画这种先后顺序呢？

2. 时间是什么

The concept of time is fundamental to our way of thinking. It is derived from the more basic concept of the order in which events occur.

时间的定义对于分布式领域关于“事件发生先后”、“并发”等概念的认识至关重要。Lamport在文中指出，时间是由更加基本的概念“事件发生的顺序”衍生出来的。例如我们说某件事在13:00发生，其实是在说这件事发生在我们读到时钟上的读数为13:00之后，13:01之前。在此种定义下，时钟其实是通过读取时刻这一行为，对连续的时间进行了离散化的编号。

3. 分布式系统

本文中讨论的分布式系统，是由若干空间上分离的process组成。同一process上的事件顺序串行发生，process之间通过收发消息进行通信。这里的process可以是若干独立的计算机，独立的进程，亦或是一台计算机内独立的硬件模块。在后文中我们我们统称process为“节点”。特别的，我们应当注意各个节点之间的通信延迟，它与单个节点内部事件发生的频率相比是不可忽略的。

4. Happened Before 偏序关系

对于一个分布式系统中的若干事件，我们定义“happened before”关系，记为"$\rightarrow$"。其满足如下三个条件，

当且仅当 $a \nrightarrow b$ 且 $b \nrightarrow a$ 时，我们称两个事件为并发的(concurrent)。

此外，我们规定 $\rightarrow$ 为非自反关系，即 $a \nrightarrow a$ 。显然，说一件事发生在自己“之前”并无任何意义。

为了直观的描述这一关系，Lamport引入了如下图所示的“时空图”，图中垂直方向自下而上为时间发生顺序，水平方向为空间上的不同节点。图中的黑色圆点表示事件，波浪线箭头表示通信消息。

回顾上面的"happened before"关系, 我们不难在图中找到若干满足条件的事件对，例如 $p_1 \rightarrow r_4$，其由 $ p_1 \rightarrow q_2 \rightarrow q_4 \rightarrow r_3 \rightarrow r_4$ 推导而来。

图中亦有若干并发的事件，例如 $p_3$ 和 $q_3$，虽然在图中我们能看到 $p_3$ 发生的物理时间(physical time)晚于 $q_3$，但对于系统中的节点来说，他们并不知道谁先谁后。

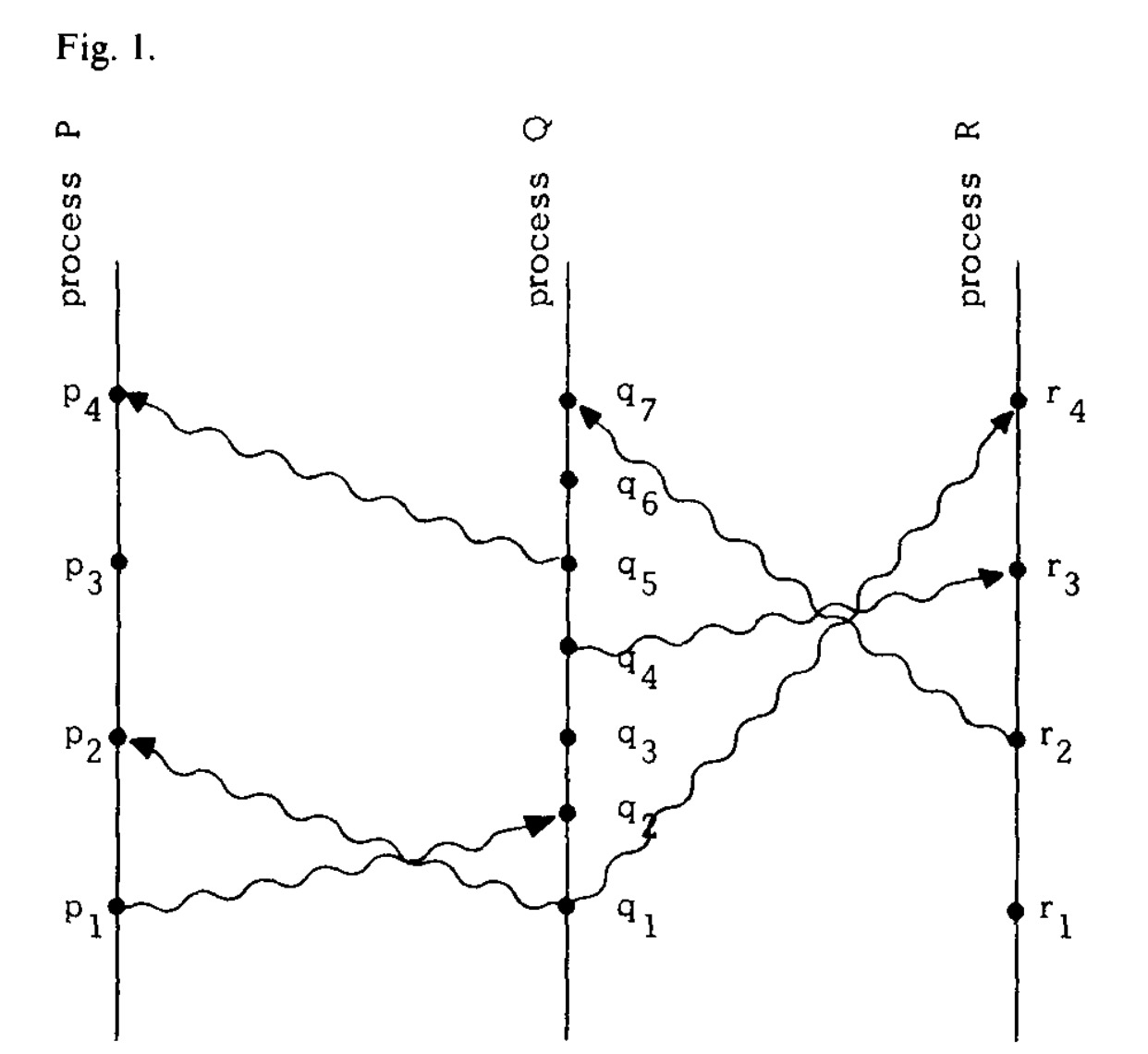
图1. space-time diagram

图1. space-time diagram

5. 逻辑时钟

a clock is just a way of assigning a number to an event.

时钟仅仅是对事件的发生予以编号而已。 更加准确地讲，对于每一个节点 $P_i$ 我们定义时钟 $C_i$ 为一个函数，它为任意的事件 $a$ 赋值编号为 $C_i \langle a \rangle$。对整个系统时钟来讲，任意事件 $b$ 的发生时间标记为 $ C \langle b \rangle $，如果其发生在节点 $P_j$ 上，则 $ C \langle b \rangle = C_j \langle b \rangle$。这里的时钟我们看做是系统内部的逻辑时钟，而非物理时钟，其标识与计数方法无需与物理时间一致。为了满足上文的"happened before"偏序关系，我们设计的逻辑时钟需要满足如下的Clock Condition.

Clock Condition. 对于系统中的任意事件 $a, b$：如果 $ a \rightarrow b$，则有 $C \langle a \rangle < C \langle b \rangle$。

特别的，Clock Condition的逆命题"如果 $C \langle a \rangle < C \langle b \rangle$，则有 $ a \rightarrow b$“并不一定成立。 因为它要求并发的事件必须具有相同的逻辑时间。例如图1中的 $p_2,p_3$ 都与 $q_3$ 为并发关系，但由 C1 有 $C \langle p_2 \rangle < C \langle p_3 \rangle$，则必然有 $C \langle q_3 \rangle \neq C \langle p_2 \rangle$ 或 $C \langle q_3 \rangle \neq C \langle p_3 \rangle$，与并发关系矛盾。

对于逻辑时钟，我们可以想象单个节点内不断发生着“tick”事件，例如在同一节点 $P_i$ 内连续发生的 $a, b$ 两个事件，有 $C_i \langle a \rangle = 4, C_i \langle b \rangle = 7$，那么在这两个事件之间发生了编号为 $5,6,7$ 的 tick 事件。于是我们可以在时空图中加入类似下图虚线所示的"tick line”。根据 C1 我们可以得到，在同一节点内的连续两个事件之间，至少要有一条 tick line。 根据 C2 我们可以得到，每一条消息必须穿过至少一条 tick line。

图2

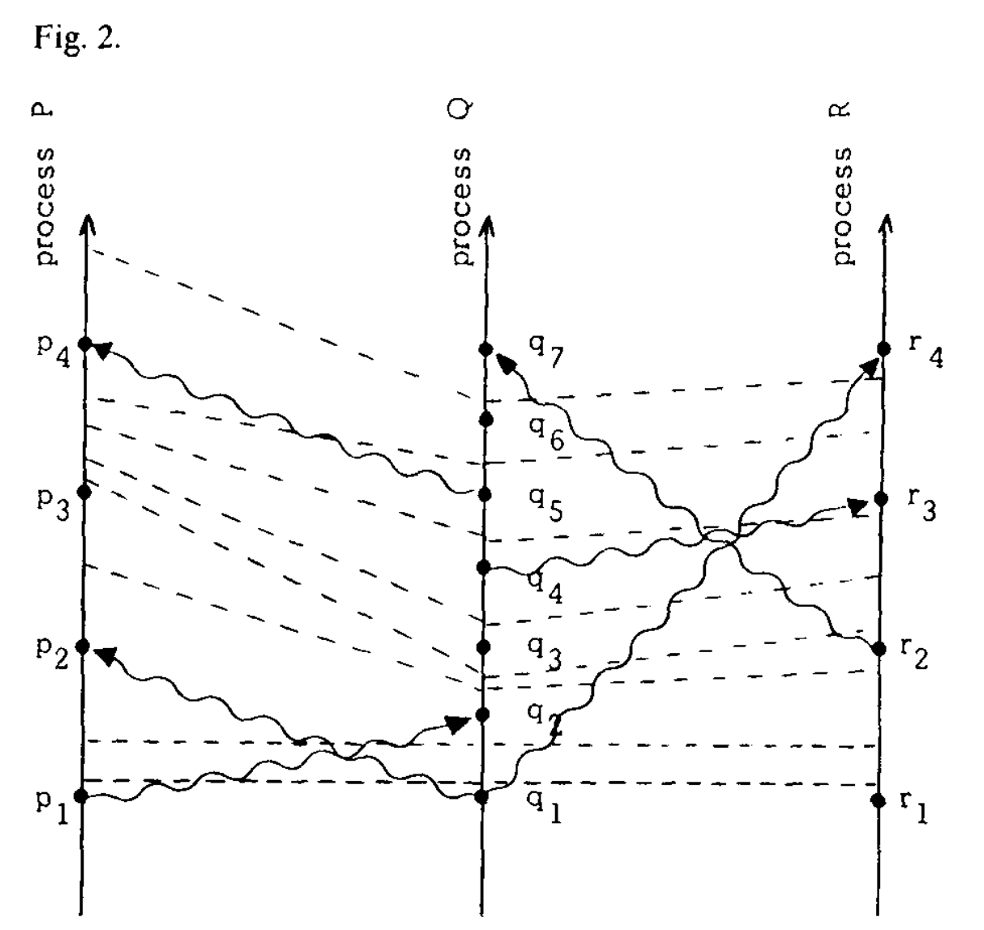
图2

为了更方便理解，我们也可以在保证事件和消息的偏序关系下，将 tick line 绘制成如下图中等价的水平线的形式。

图3

图3

对于单个节点上的逻辑时钟算法的实现，我们有如下的实现规则（Implementation Rule）：

在实践中，当我们收到某条消息后，应当先执行 IR2 修改时间，再执行具体事件，从而保证 Clock Condition。

6. 全序关系

利用逻辑时钟，我们可以对整个系统中的事件进行全序(total order)排序。我们首先根据事件发生的逻辑时间对其排序。对于发生时间相同的事件，我们引入对于所有节点的预先优先级 $\prec$，这里的优先级可以是根据 id 排序等任意规则。

更加严谨的说，我们定义全序关系 $\Rightarrow$。对于发生在节点 $P_i$ 的事件 $a$ 和发生在节点 $P_j$ 的事件 $b$，有 $ a \Rightarrow b $ 当且仅当 (i) $ C_i \langle a \rangle < C_j \langle b \rangle $ 或 (ii) $C_i \langle a \rangle = C_j \langle b \rangle$ 且 $P_i \prec P_j$。

这里由 Clock Condition 我们可以看到，凡是满足偏序关系 $\rightarrow$ 的，一定也满足全序关系 $\Rightarrow$。

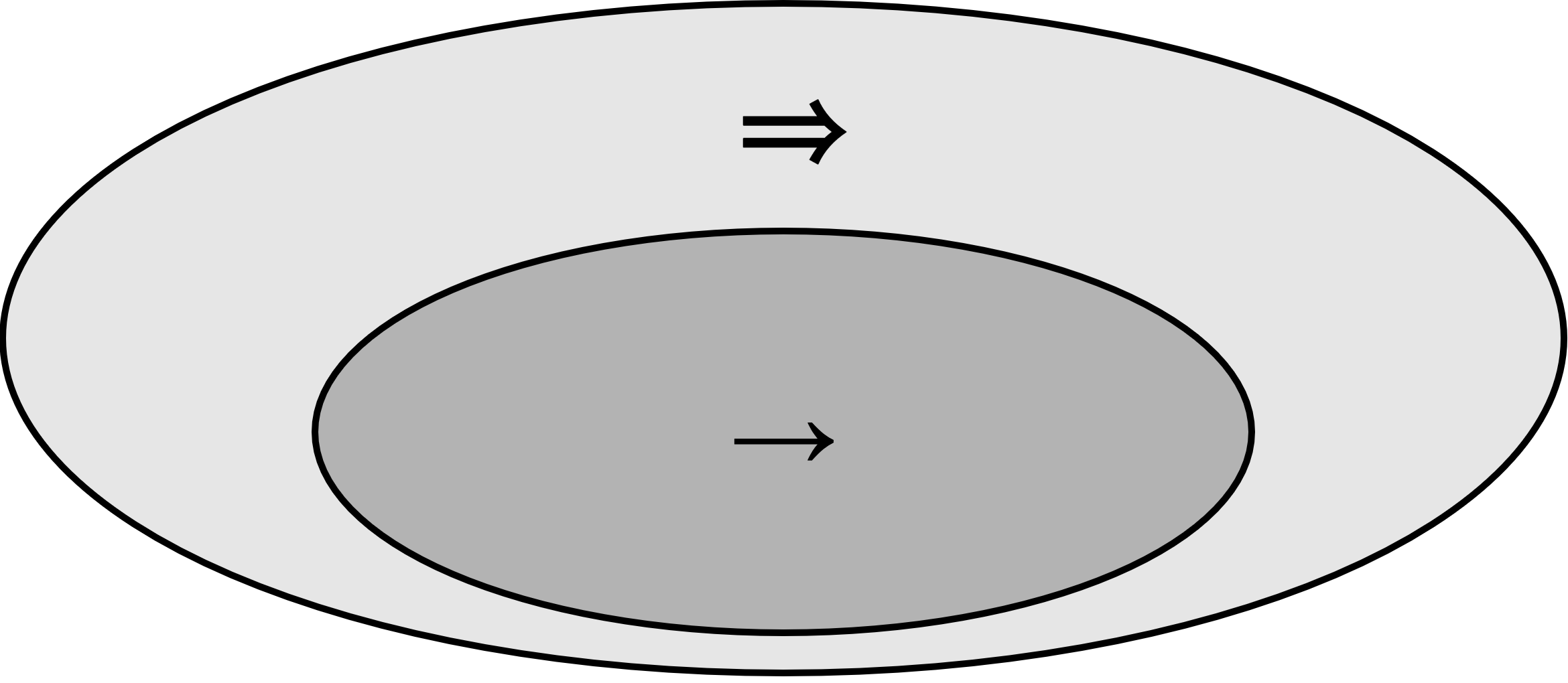
图4. 偏序与全序关系

图4. 偏序与全序关系

7. 物理时钟

7.1 系统之外

在全序关系下，由于系统之外的一些事件，使得我们有时会遇到一些反常行为。

考虑下面这种情况，某人在节点A上触发了事件A，随后打电话给另一个人。此人接到电话后在节点B上触发事件B。由于整个系统对于系统之外的事件“打电话”毫不知情，则有可能出现 $B \Rightarrow A$ 的情况。

我们可以定义系统中的所有事件集合为 $\varphi$。系统中的事件与外部事件的合集为 $\underline{\varphi}$。$\underline{\rightarrow}$ 为 $\underline{\varphi}$ 上的 happened before 关系。在上面的例子中，我们有 $A \underline{\rightarrow} B$，但 $A \nrightarrow B$。

显然没有任何算法能够不利用外部信息，仅凭 $\varphi$ 就能保证 $\underline{\rightarrow}$ 关系。在此，为了能够确保$A \rightarrow B$，有如下两种方案，

  1. 显式的引入外部信息。例如 $A$ 事件发生的逻辑时间为 $T_A$，在接到电话后，显式的告知系统 $B$ 的发生时间应大于 $T_A$。
  2. 构建满足如下Strong Clock Condition 的系统。

Strong Clock Condition. 对于 $\varphi$ 中的任意事件 $a, b$：如果$ a \underline{\rightarrow} b$ 则 $C \langle a \rangle < C \langle b \rangle$。

显然相较于方案1，Strong Clock Condition才是我们希望的方案。下面具体介绍如何实现满足Strong Clock Condition的物理时钟。

7.2 物理时钟实现

令 $C_i(t)$ 表示时钟 $C_i$ 在物理时间 $t$ 读到的读数。为了数学上的方便起见，在此我们认为 $C_i$ 对于 $t$ 是连续可微的，$dC_i(t)/dt$ 表示时钟在时间 $t$ 运行的速率。

为了使 $C_i$ 的运行速率与真实物理时钟相近，对于所有的 $t$，我们必须使得 $dC_i(t)/dt \approx 1$。更严谨的讲，我们需要满足如下条件，

除了保证单个时钟运行准确之外，各个时钟之间也需要保持同步，即所有的 $i,j,t$，有 $C_i(t) \approx C_j(t)$，

对于 PC2，由于累计误差(accumulated error)的存在，两个完全独立运行的时钟必然会误差越来越大。因此我们需要某种算法对不同节点上的时钟进行对时。

首先我们假设我们的时钟满足Clock Condition.，这样我们只需考虑在 $\underline{\varphi}$ 中 $a \nrightarrow b$ 的情况。不难发现，此时 $a$ 与 $b$ 必然发生在不同的节点上。

令 $\mu$ 小于节点间的最小通信时延。即事件 $a$ 发生于物理时间 $t$，事件 $b$ 发生于另一节点，若 $ a\underline{\rightarrow} b$，则 $b$ 最早发生于 $t + \mu$。通常我们可以设定 $\mu$ 为节点间的最小距离除以光速。

为了避免上文中的反常情况，我们必须保证对于任意的 $i, j$ 和 $t$ ，有 $C_i(t + \mu) - C_j(t) > 0$。

结合PC1. 有 $C_i(t + \mu) - C_i(t) > (1- \kappa)\mu$，详细推导见附录8.2。

结合PC2. 有需保证 $ -\epsilon \geq -\mu(1 - k)$，则需有 $\epsilon/(1 - \kappa) \leq \mu$，详细推导见附录8.3。

7.2.1 物理时钟算法

下面介绍具体的的算法实现，从而保证上面的公式与PC1，PC2成立。

对于一条发送于物理时间 $t$ ，接收于物理时间 $t’$ 的消息 $m$。我们定义消息的总延迟（total delay） $ v_m = t’ - t$。接受消息的节点当然不知道 $v_m$ 的值，但是它可以知道这条消息的最小延迟（minimum delay） $\mu_m$， $\mu_m \geq 0$ 且 $\mu_m \leq v_m$。我们称 $\xi_m = v_m - \mu_m$ 为不可预测延迟（unpredictable delay）。

对于单个节点上的物理时钟算法的实现，我们有如下的实现规则（Implementation Rule）：

7.2.1 物理时钟算法证明

现在我们证明上述的实现规则可以确保满足PC2。

将整个系统视为一个有向图，图中的点为各个节点，$P_i$ 到 $P_j$ 的有向边视为其消息链路。

令 $d$ 为有向图的直径(longest shortest path)。$\tau$ 为两个节点之间的最低通信间隔，即任意时间 $t$ 到 $t + \tau$之间，$P_i$ 至少应该发送一条消息给 $P_j$。下面的定理给出系统启动后，至多多久系统会达成满足PC2的时间同步。

定理：假设系统为一个遵循IR1’和IR2’，且直径为 $d$ 的强连通图。对于任意的消息 $m$，$\mu_m \leq \mu$，其中$\mu$ 为某个特定常数，且对于所有 $t \geq t_0$。 (a) PC1 总是成立。 (b) 存在常数 $\tau$ 和 $\xi$，在系统中每条边上，每$\tau$秒会转发一条不可预测延迟最大为 $\xi$ 的消息。则PC2 满足于，对于所有的 $t\gtrapprox t_0 + \tau d$，$\epsilon \approx d(2\kappa\tau + \xi)$，$\mu + \xi \ll \tau$。其证明见于附录8.4。

8.附录

8.1 全序关系的应用：互斥访问

  1. 资源必须要在正在访问它的节点释放后，才可以分配给其他节点访问。
  2. 按节点请求的顺序访问资源，先到先得。
  3. 如果每个访问资源的节点最终都会释放资源，那么所有请求访问的节点最终都可以成功访问。

8.2 PC1 推导

由PC1有 $\left | \frac{C_i(t+\mu) - C_i(t)}{\mu} < \kappa \right |$，则有 $(1 - \kappa)\mu < C_i(t+\mu) - C_i(t) < (1 + \kappa)\mu$ 。

8.3 PC2 推导

继8.2有，$C_i(t) + \mu(1-k) < C_i(t+\mu)$。

故要使得 $C_i(t + \mu) - C_j(t) > 0$，则需有 $C_i(t) - C_j(t) > -\mu(1 - k)$。

由PC2有，$C_i(t) - C_j(t) < -\epsilon$。

故而得，$ \epsilon \leq \mu(1 - k)$。

8.4 定理证明

对于任意的 $i$ 和 $t$，我们定义 $C_i^t$ 为一时钟，在时刻 $t$ 设定为 $C_i$ 并与 $C_i$ 运行速率相同，且永不被修正(reset)。即，

$$ C_i^t = C_i(t) + \int_{t}^{t’}[dC_i(t)/dt]dt \tag{1}$$

对于所有的 $t’ \geq t$，我们注意到由于 $C_i$ 会被修正，有

$$ C_i(t’) \geq C_i^t(t’) \tag{2}$$

假设 $P_1$ 在时刻 $t_1$ 发送消息给 $P_2$，接收于时刻 $t_2$，不可预测延迟 $\leq \xi$，$ t_0 \leq t_1 \leq t_2$。则对于所有的 $t \geq t_2$，我们有

$$ \begin{aligned} & C_2^{t_2}(t) \geq C_2^{t_2}(t_2) + (1 - \kappa)(t - t_2) & \qquad [by\ (1)\ and\ PC1] \\ & \geq C_1(t_1) + \mu_m + (1 - \kappa)(t - t_2) & \qquad [by\ IR2’(b)] \\ & = C_1(t_1) + (1 - \kappa)(t - t_1) - [(t_2 - t_1) - \mu_m] + \kappa(t_2 - t_1) \\ & \geq C_1(t_1) + (1 - \kappa)(t - t_1) - \xi \end{aligned} $$

因此，利用这些假设，我们可以得到，对于所有的$t \geq t2$，有

$$ C_2^{t_2}(t) \geq C_1(t_1) + (1 - \kappa)(t - t_1) - \xi \tag{3} $$

现在假设对于 $i =1,…,n$，我们有$ t_i \leq t_i’ < t_{i+1}, t_0 \leq t_1$。在 $t_i’$时，$P_i$ 发送一条消息给 $P_{i+1}$，该消息接收于 $t_{i+1}$，其不可预测延迟小于 $\xi$。反复应用等式(3)可以得到，对于 $t \geq t_{n+1}$，

$$ C_{n+1}^{t_{n+1}}(t) \geq C_1(t_1’) + (1 - \kappa)(t - t_1’) - n\xi \tag{4} $$

通过 PC1, IR1’, IR2’我们可以推导出，

$$ C_1(t_1’) \geq C_1(t_1) + (1 - \kappa)(t_1’ - t_1) $$

再结合(4)与(2)，我们可以得到对于 $t \geq t_{n+1}$，有

$$ C_{n+1}(t) \geq C_1(t_1) + (1 - \kappa)(t - t_1) - n\xi \tag{5} $$

对于任意的两个节点 $P$ 和 $P’$，我们能找到一个节点序列 $P = P_0, P_1, …, P_{n+1} = P’, n \leq d$。通过假设 (b)，我们能找到时间 $t_i, t_i’$，有 $ t_i’ - t_i \leq \tau $ 且 $ t_{i+1} - t_i’ \leq v $，其中 $v=\mu + \xi$。因此不等式 (5) 成立于对于任何的$t \geq t_1 + d(\tau + v)$, 有$ n \leq d$。对于任意的$i, j, t, t_1$，其中 $ t_1 \geq t_0 $ 且 $ t \geq t_1 + d(\tau + v) $，我们因此有

$$ C_i(t) \geq C_j(t_1) + (1 - \kappa)(t - t_1) - d\xi \tag{6} $$

令 $m$ 为任意时间戳为 $T_m$ 的消息，其在 $t$ 时刻发送，在 $t’$ 时刻接收。我们假设 $m$ 有一个以一个恒定速率运行的时钟 $C_m$，且有 $C_m(t)=t_m$，$C_m(t’) = t_m + \mu_m$。那么由 $ \mu_m \leq t’ - t $ 可以推导出 $dC_m/dt \leq 1$。规则 IR2’(b)将 $C_j(t’)$ 设置为 $max(C_j(t’ - 0), C_m(t’))$。因此，当时钟被重置时，只可能重置与其他某个时钟相等。

对于任意时间 $t_x \geq t_0 + \mu/(1-\kappa)$，令 $C_x$ 为 $t_x$ 时刻具有最大值的时钟。由于所有的时钟以低于 $1+\kappa$ 的速率运行，我们有对于所有的 $i$ 和所有的 $t \geq t_x$：

$$ C_i(t) \leq C_x(t_x) + (1 + \kappa)(t - t_x) \tag{7} $$

现在我们考虑如下两种情况：（i）$C_x$ 为节点 $P_q$ 的时钟 $C_q$。（ii）$C_x$ 为节点 $P_q$ 在 $t_1$ 时刻发送于消息 $m$ 的时钟。在情况（i）中，(7)简单的成为，

$$ C_i(t) \leq C_q(t_x) + (1 + \kappa)(t - t_x) \tag{8i} $$

在情况（ii）中，由于 $C_m(t_1)=C_q(t_1)$，且 $dC_m/dt \leq 1$，我们有，

$$ C_x(t_x) \leq C_q(t_1) + (t_x - t_1) $$

因此，由(7)有，

$$ C_i(t) \leq C_q(t_1) + (1 - \kappa)(t - t_1) \tag{8ii} $$

由于 $t_x \geq t_0 + \mu/(1 - \kappa)$，我们有，

$$ \begin{aligned} & C_q(t_x - \mu/(1 - \kappa)) \leq C_q(t_x) - \mu & \qquad [by\ PC1] \\ & \leq C_m(t_x) - \mu & \qquad [by\ choice \ of \ m] \\ & \leq C_m(t_x) - (t_x - t_1)\mu_m/v_m & \qquad [\mu_m \leq \mu, t_x - t_1 \leq v_m] \\ & = T_m & \qquad [by\ definition \ of \ C_m] \\ & = C_q(t_1) & \qquad [by\ IR2’(a)] \end{aligned} $$

因此，$ C_q(t_x - \mu/(1 - \kappa)) \leq C_q(t_1) $，因此 $ t_x - t_1 \leq \mu(1 - \kappa), t_1 \geq t_0 $。

令 $ t_1 = t_x $，对于情况(i)，我们结合(8i)和(8ii)可以推出对于任意的 $t，t_x$，且$t \geq t_x \geq t_0 + \mu/(1 - \kappa)$，存在一个节点 $P_q$ 和一个时间 $t_1$，$t_x - \mu/(1 - \kappa)\leq t_1 \leq t_x$，对于所有的 $ i $，

$$ C_i(t) \leq C_q(t_1) + (1 + \kappa)(t - t_1) \tag{9} $$

若我们选择的 $t$ 和 $t_x$ 满足 $t \geq t_x + d(\tau + v)$，我们可以结合（6）和（9）得到存在一个时间 $t_1$ 和一个节点 $P_q$，对于所有的 $i$，

$$ C_q(t_1) + (1 - \kappa)(t - t_1) - d\xi \leq C_i(t) \leq C_q(t_1) + (1 - \kappa)(t - t_1) \tag{10} $$

令 $t = t_x + d(\tau + v)$，我们有,

$$ d(\tau + v) \leq t - t_1 \leq d(\tau + v) + \mu(1 - \kappa) $$

结合（10），我们有，

$$ C_q(t_1) + (t - t_1) - \kappa d(\tau + v) - d\xi \leq C_i(t) \leq C_q(t_1) + (t - t_1) + \kappa[d(\tau + v) + \mu/(1 - \kappa)] \tag{11} $$

结合假设 $\kappa \ll 1$ 以及 $\mu \leq v \ll \tau$，我们可以重写（11）为，

$$ C_q(t_1) + (t - t_1) - d(\kappa\tau + \xi) \lessapprox C_i(t) \lessapprox C_q(t_1) + (t - t_1) + d\kappa\tau \tag{12} $$

由于上式对于所有的 $i$ 成立，我们有，

$$ |C_i(t) - C_j(t)| \lessapprox d(2\kappa\tau + \xi) $$

上式对于所有的 $t \gtrapprox t_0 + d\tau $ 均成立。

证毕。