在之前的文章中提到过Dijkstra于1965年提出的基于共享存储的临界区互斥访问问题。Dijkstra提出了基于对内存单元的原子性读写实现的方案。然而，Lamport指出Dijkstra的方案会因为节点在临界区内失效而导致系统死锁。在其于1974年发表的文章A New Solution of Dijkstra’s Concurrent Programming Problem中，Lamport提出了完全基于软件实现的解决方案，被称为“面包店算法”。

面包店算法

”面包店算法"模拟面包店内取号服务的模式，实现了先来先服务的的互斥访问。我们有如下说明，

如果不同节点对同一内存单元并发读写，只有写会正确执行，读可能会读到不确定值。
节点失效时，其立即跳转至其非临界区并挂起。其后一段时间内读取其内存会返回不确定值，最终所有的读会返回0。
使用初始值为0的两个数组choosing[1:N] 和 number[1:N]，其中N为节点数量。
number[i] 的取值没有上限。
代码中 maximum 函数读到各个变量的值的顺序没有要求。
代码 L3 中的比较运算 (a,b)<(c,d) 可以视为 if a < c or if a = c and b < d。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


begin integer j;
  L1: choosing[i] := 1;
      number[i] := 1 + maximum(number[1], ... , number[N]);
      choosing[i] := 0;
      for j = 1 step 1 until N do
        begin
          L2: if choosing[j] != 0 then goto L2;
          L3: if number[j] != 0 and (number[j], j) < (number[i], i) then goto L3;
        end;
      critical section;
      number[i] := 0;
      noncritical section;
      goto L1;
end

证明

对于节点 i ，在第2行将 choosing[i] 设置为1后，称其进入“门廊(doorway)”。在第4行将 choosing[i] 设置为0后，直至其失效(fail)或完成第11行离开临界区前，我们称其进入“面包店(bakery)”内。我们有如下断言，

断言1：对于已经在面包店内的两个节点 i 和 k 。如果在 i 进入面包店的时间早于 k 进入门廊的时间，则有 number[i] < number[k]。

证明：在 k 运行第3行设定 number[k] 时，由于 i 已进入面包店，所以 number[i] 已经被设定，且直至 i 离开面包店不再更改。故number[k] >= 1 + number[i]。

断言2：如果节点 i 在临界区内，k 在面包店内，且 k != i，则有 (number[i], i) < (number[k], k)

证明：由于 choosing[k] 本质上只有0和1两个值，我们可以假定从节点 i 的角度来看，对于 choosing[k] 的读写是瞬间完成的，不存在同时的读写。例如下图，节点 i 正在读取 choosing[k], 此时节点 k 正在将其从0写为1。如果 i 读到的是0，则认为读先发生。如果读到的是1，则认为读后发生。

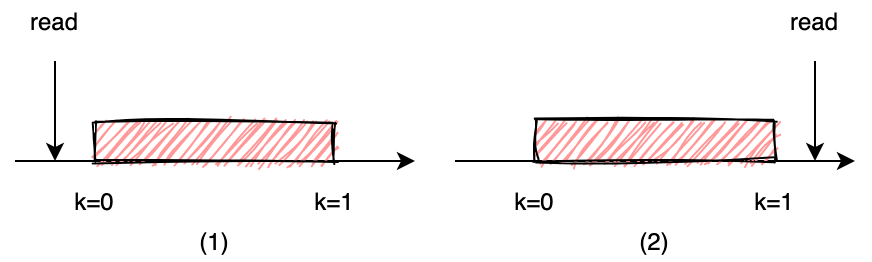
由于 i 已经进入其临界区，我们令，

$ t_{L2} $ 为 i 在 L2 处读取到 choosing[k] = 0 的时间。
$ t_{L3} $ 为 i 在 L3 处最后一次和 number[k] 比较的时间。

则有 $ t_{L2} < t_{L3} $。

在 k 进入面包店前执行 L1 设定当前的 number[k] 过程中，令，

$ t_e $ 为 k 执行完成第2行，进入门廊的时间。
$ t_w $ 为 k 执行完成第3行设定 number[k] 的时间。
$ t_c $ 为 k 执行完成第4行离开门廊的时间。

则有 $ t_e < t_w < t_c $。由于 $ t_{L2} $ 时 choosing[k] = 0，所以可能有如下两种可能，

$ t_{L2} < t_e $ ，在k进入门廊前，读到 choosing[k] = 0。
$ t_{L2} > t_c $ ，在k进入面包店后，读到 choosing[k] = 0。

情况1为断言1中情况，故number[i] < number[k]。

情况2时，有$ t_e < t_w < t_c < t_{L2} < t_{L3} $，所以$ t_w < t_{L3} $。在 i 执行 L3 中 j = k 时，i可以读取到 number[k] 的值，且随后只会循环阻塞在大于 k 的 j 上。所以此时有 (number[i], i) < (number[k], k)。

断言3：假设只会发生一定数量的节点失效，即没有节点不断fail-recover-fail。而且失效的节点中没有节点在其临界区中，且至少有一个没有失效的节点在面包店内。那么一定存在某个节点最终能进入其临界区。

证明：假设还没有任何节点进入过临界区，那么在一段时间后，一定会不再有节点进出面包店。此时，假设节点 i 拥有最小的号码 (number[i], i)，那么其会完成 L3 中的循环，进入临界区。

断言2证明了在面包店内，只能有一个节点在临界区内。断言1和断言2证明了算法为”先来先服务(first-come-first-served)“。断言3说明只有当某个节点在其临界区内失效时或某些节点持续失效时，系统才会产生死锁。

在节点 j 持续失效的情况中，i 也许会发现 choosing[j] = 1 从而block在 L2。

最后

谢谢你的阅读。如果你读过本文后有任何的思考或疑虑，请务必让我知道。

A New Solution of Dijkstra’s Concurrent Programming Problem, Lamport, 1974

2020/09/05

面包店算法

证明

最后